Sorteren is een basisbewerking waarbij de elementen van een array in een bepaalde volgorde worden gerangschikt om de zoekbaarheid te vergroten. In eenvoudige bewoordingen worden de gegevens gesorteerd zodat deze gemakkelijk kunnen worden doorzocht.
Vergelijkingstabel
| Basis voor vergelijking | Invoegsortering | Selectie Sorteren |
|---|---|---|
| basis- | De gegevens worden gesorteerd door de gegevens in een bestaand gesorteerd bestand in te voegen. | De gegevens worden gesorteerd door de opeenvolgende elementen op de gesorteerde locatie te selecteren en te plaatsen. |
| Natuur | Stal | wankel |
| Proces dat moet worden gevolgd | Elementen zijn van tevoren bekend, terwijl de locatie waarnaar ze moeten worden doorzocht. | Locatie is eerder bekend terwijl elementen worden doorzocht. |
| Onmiddellijke gegevens | Invoegsortering is live sorteringstechniek die onmiddellijke gegevens kan verwerken. | Het kan niet omgaan met onmiddellijke gegevens, het moet in het begin aanwezig zijn. |
| Beste casuscomplexiteit | Op) | O (n 2 ) |
Definitie van invoegsortering
Insertion sort werkt door de set waarden in het bestaande gesorteerde bestand in te voegen. Het construeert de gesorteerde array door één element tegelijk in te voegen. Dit proces gaat door totdat de hele array in een bepaalde volgorde is gesorteerd. Het primaire concept achter invoegselectie is om elk item op de juiste plaats in de definitieve lijst in te voegen. De invoegsorteermethode bespaart een effectieve hoeveelheid geheugen.
Werking van het invoegsorteertype
- Het maakt gebruik van twee reeksen arrays waarin de gesorteerde gegevens en andere op ongesorteerde gegevens worden opgeslagen.
- Het sorteeralgoritme werkt totdat er elementen in de ongesorteerde set staan.
- Laten we aannemen dat er 'n' nummerelementen in de array zijn. Aanvankelijk bestaat het element met index 0 (LB = 0) in de gesorteerde set. Resterende elementen staan in de ongesorteerde partitie van de lijst.
- Het eerste element van het ongesorteerde gedeelte heeft matrixindex 1 (If LB = 0).
- Na elke iteratie kiest het het eerste element van de ongesorteerde partitie en voegt het in op de juiste plaats in de gesorteerde set.
Voordelen van Insertion sort
- Eenvoudig geïmplementeerd en zeer efficiënt bij gebruik met kleine sets gegevens.
- De extra vereiste geheugenruimte voor invoegsortering is minder (dwz O (1)).
- Het wordt beschouwd als live-sorteringstechniek, omdat de lijst kan worden gesorteerd terwijl de nieuwe elementen worden ontvangen.
- Het is sneller dan andere sorteeralgoritmen.
Voorbeeld:
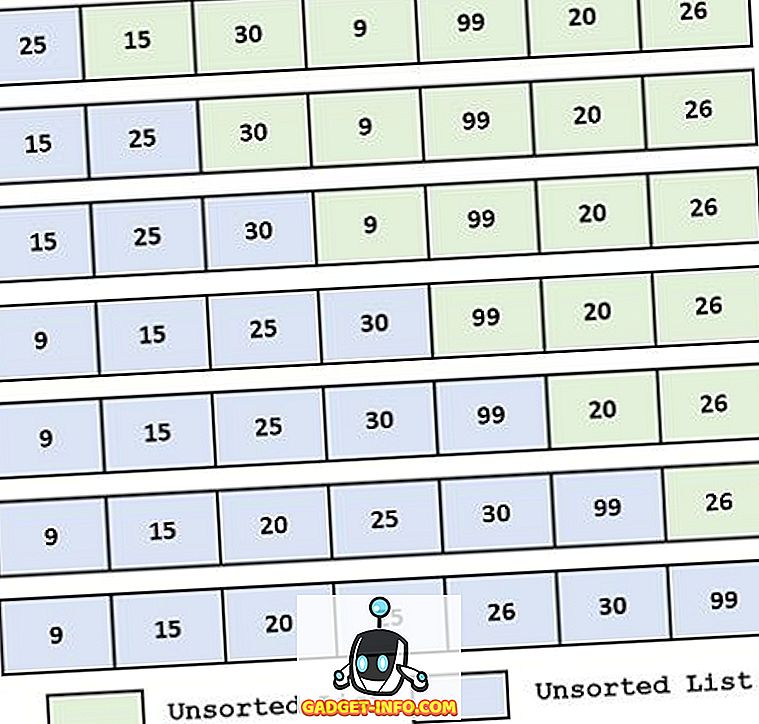
Definitie van selectiesortering
De sortering sorteren sorteert door te zoeken naar het minimumwaardegetal en deze in de eerste of laatste positie te plaatsen volgens de volgorde (oplopend of aflopend). Het zoeken naar de minimum sleutel en het in de juiste positie plaatsen gaat door totdat alle elementen op de juiste plaats zijn geplaatst.
Werking van de selectiesortering
- Stel dat een array ARR met N-elementen in het geheugen staat.
- In de eerste passage wordt de kleinste sleutel samen met de positie doorzocht en vervolgens wordt de ARR [POS] geruild met ARR [0]. Daarom is ARR [0] gesorteerd.
- In de tweede passage wordt opnieuw de positie van de kleinste waarde bepaald in de subreeks van N-1 elementen. Wissel de ARR [POS] uit met ARR [1].
- In de doorgang N-1 wordt hetzelfde proces uitgevoerd om het N-aantal elementen te sorteren.
Voorbeeld:
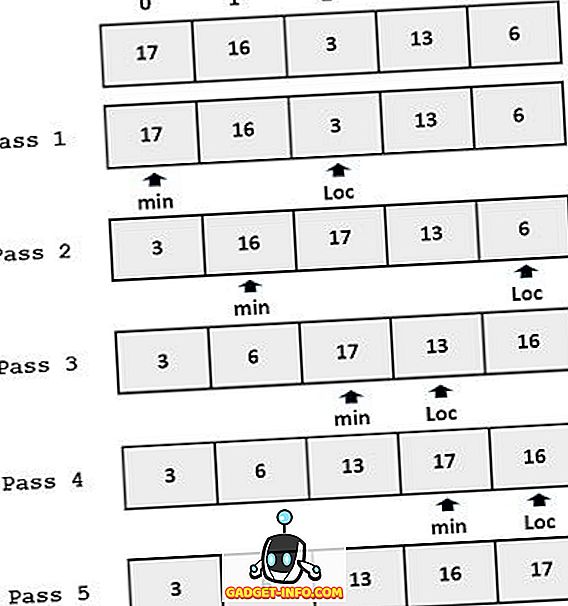
Belangrijkste verschillen tussen Insertion Sort en Selection Sort
- Het invoegsorteerproces voert meestal de invoegbewerking uit. Integendeel, de selectie sorteert de selectie en positionering van de vereiste elementen.
- Insertion sort is stabiel, terwijl selectiesortering geen stabiel algoritme is.
- In het invoegsorteeralgoritme zijn de elementen eerder bekend. De selectiesortering daarentegen bevat de locatie van tevoren.
- Insertion sort is een live-sorteertechniek waarbij de aankomende elementen onmiddellijk in de lijst worden gesorteerd, terwijl het sorteren van selecties niet goed kan werken met onmiddellijke gegevens.
- Het invoegsorteertype heeft de O (n) -looptijd in het beste geval. Daarentegen is de beste casuslooptijdcomplexiteit van selectiesortering O (n2).
Complexiteit van invoegsoorten
De beste casuscomplexiteit van invoegsortering is O (n) keer, dat wil zeggen wanneer de array eerder is gesorteerd. Op dezelfde manier, als de array in omgekeerde volgorde wordt gesorteerd, moet het eerste element van de ongesorteerde array worden vergeleken met elk element in de gesorteerde set. In het slechtste geval is de invoertijd van invoegtypen dus kwadratisch, dwz O (n2) . In het gemiddelde geval moet het ook de minimale (k-1) / 2-vergelijkingen maken. Daarom heeft het gemiddelde geval ook een kwadratische looptijd O (n2).
Complexiteit van de selectiesortering
Als de werking van de selectie, sorteren is niet afhankelijk van de oorspronkelijke volgorde van de elementen in de array, dus er is niet veel verschil tussen de beste case en worst case complexiteit van selectie sorteren.
De selectiesortering selecteert het element met de minimale waarde, in het selectieproces wordt het aantal elementen 'n' gescand; daarom worden n-1 vergelijkingen gemaakt in de eerste doorgang. Vervolgens worden de elementen verwisseld. Op dezelfde manier in de tweede doorgang ook om het tweede kleinste element te vinden, hebben we het scannen van rust n-1 elementen nodig en het proces wordt voortgezet totdat de gehele reeks is gesorteerd.
Aldus is de looptijdcomplexiteit van selectiesortering O (n2) .
= (n-1) + (n-2) + ......... .. + 2 + 1
= n (n-1) / 2 = O (n2)
Conclusie
Van beide van het sorteeralgoritme is de invoegselectie snel, efficiënt, stabiel terwijl selectie sorteren alleen efficiënt werkt wanneer het een kleine set elementen betreft of de lijst gedeeltelijk eerder is gesorteerd. Het aantal vergelijkingen dat wordt gemaakt door selectie, is groter dan de uitgevoerde bewegingen, terwijl bij invoegselectie het aantal keren dat een element wordt verplaatst of verwisseld groter is dan de gemaakte vergelijkingen.