Het verschil tussen correlatie en regressie is een van de veelgestelde vragen in interviews. Bovendien lijden veel mensen dubbelzinnig in het begrijpen van deze twee. Dus, lees dit artikel volledig om een goed begrip van deze twee te hebben.
Vergelijkingstabel
| Basis voor vergelijking | Correlatie | regressie |
|---|---|---|
| Betekenis | Correlatie is een statistische maat die de co-relatie of associatie van twee variabelen bepaalt. | Regressie beschrijft hoe een onafhankelijke variabele numeriek gerelateerd is aan de afhankelijke variabele. |
| Gebruik | Een lineair verband tussen twee variabelen weergeven. | Om een beste lijn te passen en een variabele te schatten op basis van een andere variabele. |
| Afhankelijke en onafhankelijke variabelen | Geen verschil | Beide variabelen zijn verschillend. |
| Duidt op | Correlatiecoëfficiënt geeft de mate aan waarin twee variabelen samen bewegen. | Regressie geeft de impact aan van een eenheidsverandering in de bekende variabele (x) op de geschatte variabele (y). |
| Doelstelling | Een numerieke waarde vinden die de relatie tussen variabelen tot uitdrukking brengt. | Om de waarden van de willekeurige variabele te schatten op basis van de waarden van de vaste variabele. |
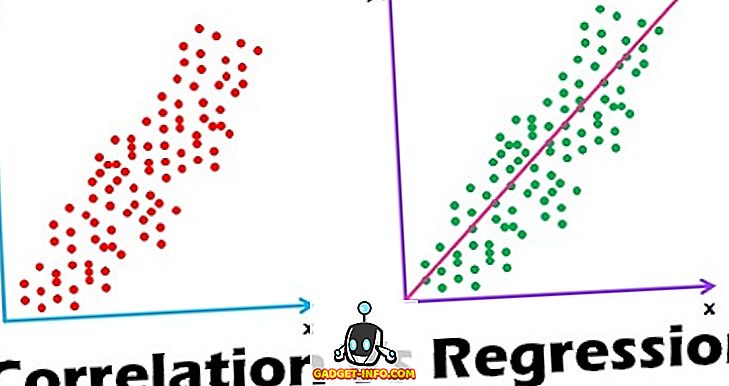
Definitie van correlatie
De term correlatie is een combinatie van twee woorden 'Co' (samen) en relatie (verbinding) tussen twee hoeveelheden. Correlatie is wanneer, op het moment van onderzoek van twee variabelen, wordt waargenomen dat een eenheidsverandering in een variabele vergeld wordt door een equivalente verandering in een andere variabele, dwz direct of indirect. Of anders wordt gezegd dat de variabelen niet-gecorreleerd zijn wanneer de beweging in één variabele niet gelijk staat aan een beweging in een andere variabele in een specifieke richting. Het is een statistische techniek die de sterkte van de verbinding tussen paren van variabelen vertegenwoordigt.
Correlatie kan positief of negatief zijn. Wanneer de twee variabelen in dezelfde richting bewegen, dwz een toename in één variabele resulteert in de overeenkomstige toename in een andere variabele en omgekeerd, dan worden de variabelen als positief gecorreleerd beschouwd. Bijvoorbeeld : winst en investeringen.
Integendeel, als de twee variabelen in verschillende richtingen bewegen, op een zodanige manier dat een toename in één variabele resulteert in een afname in een andere variabele en vice versa, wordt deze situatie negatieve correlatie genoemd. Bijvoorbeeld : prijs en vraag van een product.
De maten van correlatie worden gegeven als onder:
- Karl Pearson's Product-moment correlatiecoëfficiënt
- Spearman's rangcorrelatiecoëfficiënt
- Verspreidingsdiagram
- Coëfficiënt van gelijktijdige afwijkingen
Definitie van regressie
Een statistische techniek voor het schatten van de verandering in de metriek-afhankelijke variabele als gevolg van de verandering in een of meer onafhankelijke variabelen, gebaseerd op de gemiddelde wiskundige relatie tussen twee of meer variabelen, staat bekend als regressie. Het speelt een belangrijke rol in veel menselijke activiteiten, omdat het een krachtige en flexibele tool is die vroeger de gebeurtenissen in het verleden, het heden of de toekomst voorspelde op basis van gebeurtenissen in het verleden of heden. Bijvoorbeeld : op basis van historische gegevens kan de toekomstige winst van een bedrijf worden geschat.
In een eenvoudige lineaire regressie zijn er twee variabelen x en y, waarbij y afhangt van x of zeggen beïnvloed door x. Hier y wordt genoemd als afhankelijk, of criterium variabele en x is onafhankelijk of voorspellende variabele. De regressielijn van y op x wordt uitgedrukt als onder:
y = a + bx
waar, a = constant,
b = regressiecoëfficiënt,
In deze vergelijking zijn a en b de regressieparameter.
Belangrijkste verschillen tussen correlatie en regressie
De onderstaande punten verklaren het verschil tussen correlatie en regressie in detail:
- Een statistische maat die de co-relatie of associatie van twee grootheden bepaalt, staat bekend als Correlation. Regressie beschrijft hoe een onafhankelijke variabele numeriek gerelateerd is aan de afhankelijke variabele.
- Correlatie wordt gebruikt om de lineaire relatie tussen twee variabelen weer te geven. Integendeel, regressie wordt gebruikt om de beste regel te passen en een variabele te schatten op basis van een andere variabele.
- In correlatie is er geen verschil tussen afhankelijke en onafhankelijke variabelen, dwz de correlatie tussen x en y is vergelijkbaar met y en x. Omgekeerd is de regressie van y op x anders dan x op y.
- Correlatie geeft de sterkte van associatie tussen variabelen aan. In tegenstelling tot regressie weerspiegelt de impact van de eenheidsverandering in de onafhankelijke variabele op de afhankelijke variabele.
- Correlatie is gericht op het vinden van een numerieke waarde die de relatie tussen variabelen tot uitdrukking brengt. In tegenstelling tot regressie waarvan het doel is om waarden van de willekeurige variabele te voorspellen op basis van de waarden van de vaste variabele.
Conclusie
Met de bovenstaande discussie is het duidelijk dat er een groot verschil is tussen deze twee wiskundige concepten, hoewel deze twee samen worden bestudeerd. Correlatie wordt gebruikt wanneer de onderzoeker wil weten of de onderzochte variabelen al dan niet gecorreleerd zijn, zo ja, wat is dan de sterkte van hun associatie. Pearson's correlatiecoëfficiënt wordt beschouwd als de beste maat voor correlatie. In regressieanalyse wordt een functionele relatie tussen twee variabelen vastgesteld om toekomstige projecties op gebeurtenissen te maken.